Mathematicians solve decades
For a long time, Kakey’s conjection, involves rotating a narrow infinite needle, who invent mathematicians so far

Sean Gladwell / Getty Images
Very little reading “Spectacular progress“Or a”Once a year“It’s the result of math. If there is good reason, then, then, if you need completely new approaches and ideas, it is related to the appearance of” Kakesya Concijecture “, how to rotate a needle in the right way.
Experts have dealt with related problems since 1917. But in a February Paper published in February, the Hong Wang Mathematician of New York, Joshua Zahl Zahl Mathematician at the University of Britain finally FROATED Three-dimensional version of Kakey’s conjection. “XXI. It is one of the main mathematical achievements of the twentieth century”, said mathematicians Eyal Lubetzky of N.Y.U. A recent Press release.
Suppose there is infinite needle on a board. You want to rotate 360 degrees now to make the tip of the needle once in each direction of the plane. To do this, you can have the needle in the middle and rotate. As it rotates, the needle covers the surface of a circle.
To help Science Journalism
If you enjoy this article, consider entering award-winning journalism Subscribe. By purchasing subscription, you are helping to ensure the future of stories about the discoveries and ideas that are conformed to today.
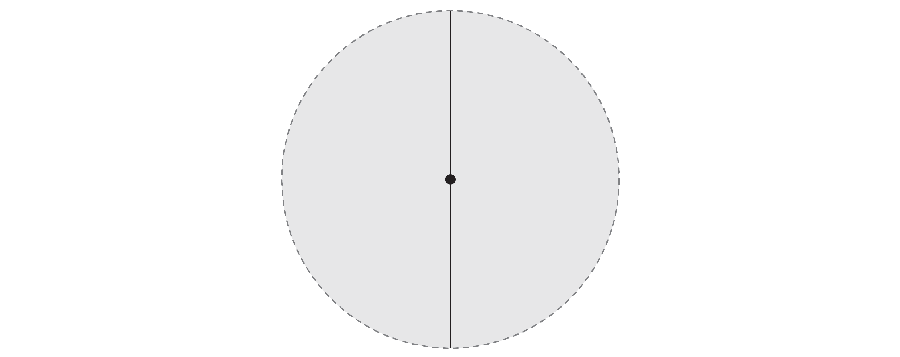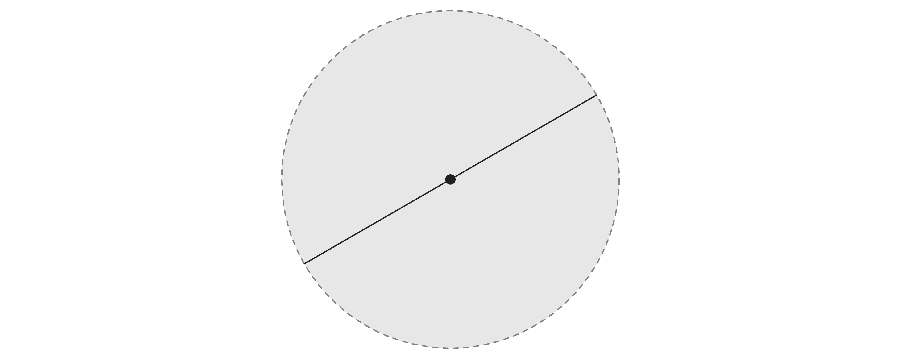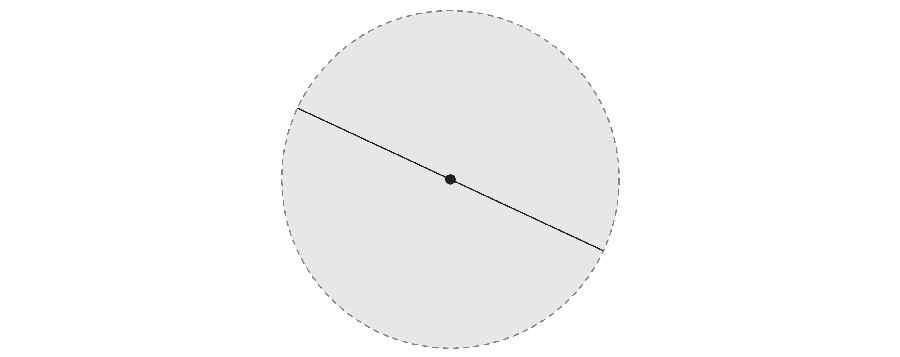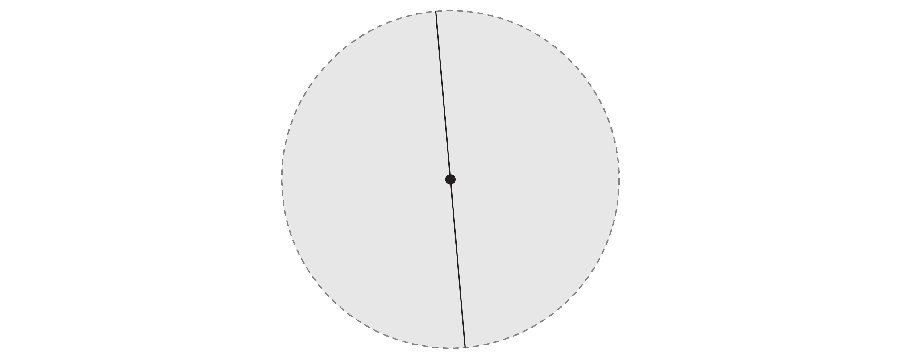
But if you are fast, the needle can make his 360-degree journey while it takes less space. In 1917 Mathematics S & OMACR; Ichi wanted to investigate the smallest area required to rotate the needle. For example, not only the outer end of the needle, but also by rotating its center, you can get the area corresponding to a triangle with a curved side.
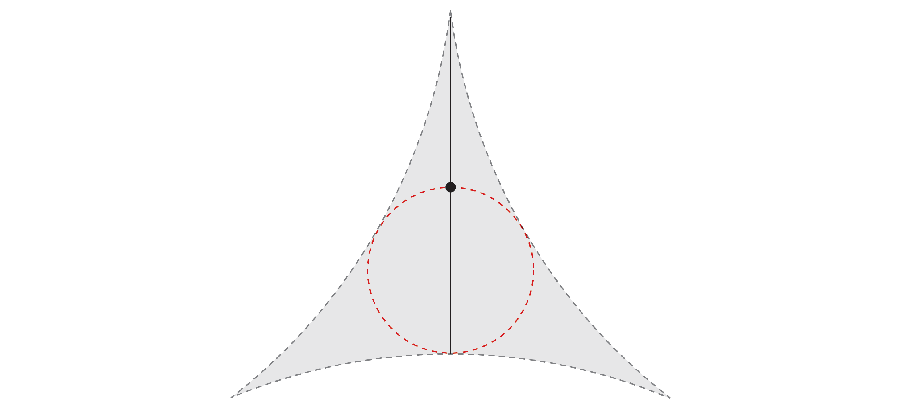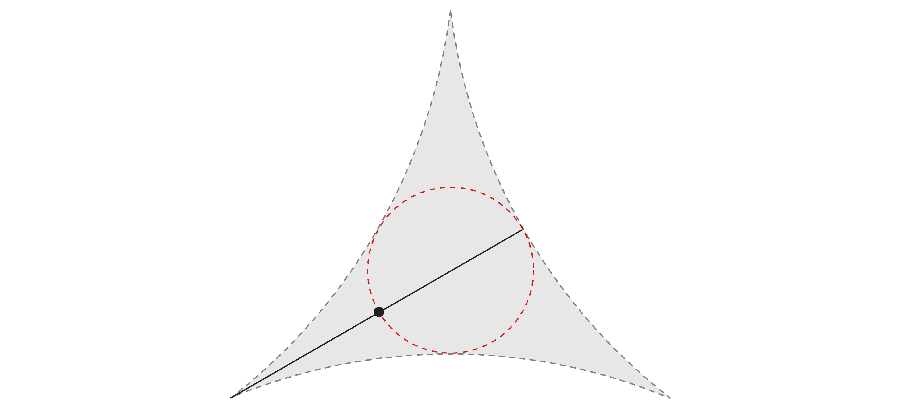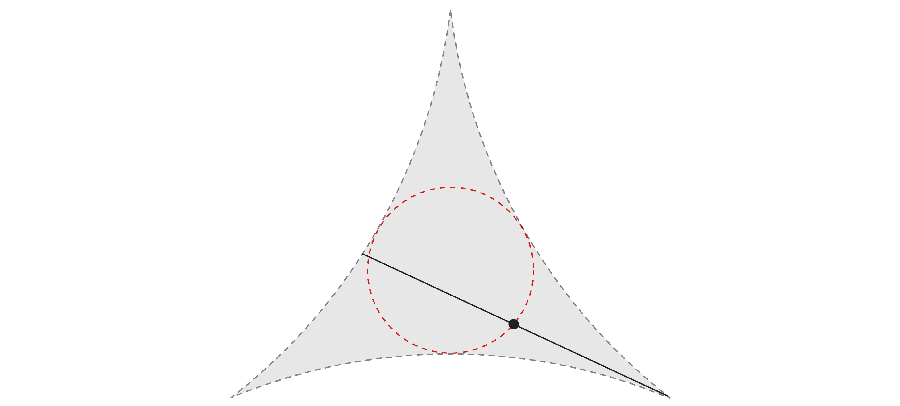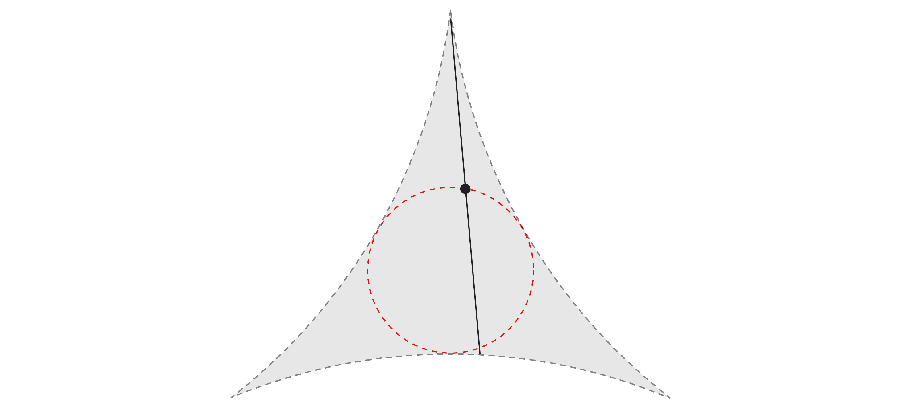
Years later, Abram Besicovitch mathematician He made an unexpected discovery. If the needle continues to move the complex maneuver in parallel parking, the tight needle coatings can have a total zero total.
Zero zero dimension?
From there, the expert began asking experts to dimensioning “Kkeya”. Usually in a plane are the surfaces, a rectangle or a circle, they are two dimensions. But there are exceptions: fractures, for example, can also have fractional measures, such as 1.5 dimensions.
Because kakey’s surfaces can be very rugged, the dimension account is obvious. In fact, it has implications in many other areas of mathematics, including harmonic analysis, which breaks complicated mathematical curves, the theory of simpler functions and geometric measures.
In fact, in 1971 the Mathematician Roy Davies could prove The Kakeya surface is always two-dimensional, even though its field disappeared. In Mathematics, however, people are interested in the general result. Experts wanted to solve the problem n Measures: Everyone makes a rotating needle n Spatial directions always cover n-Insionession volume? This hypothesis is known as Kkey Conjectures.
The three-dimensional case has been very hard to crack. Over the decades, experts could discard the option that cover the volume with less than 2.5 spatial dimensions, but they achieved that as far as they achieved.
Wang and Zahl were not recommended, however, they moved forward step by step. Through a strict effort, the gradual covered volume managed to remove all cases that would have less than three dimensions.
Thus, in the end, the Kakesya conjecturium were able to prove in three spatial dimensions, which shows the volume covered by the needle is always a three-dimensional. In the last press release, Nyuku Guido de Filippis commented: “I hope their ideas will bring a range of exciting progress in the coming years.”
This article originally appeared Science spectrum and reproduced with permission.

