Mathematicians found a 122-year-old triangular square-square-puzzle
Finally fixed the mystery fixed

Shape illustration Variable polygons.
About a decade ago TonorosNow, the Mathematician Institute of Japanese Science and Technology (JAIST) was facing an exhibition of the Museum of Music Museum Museum. A triangular interior appeared, cut into four pieces connected through small heging. With a simple rotary, parts to transform the triangle into a square.
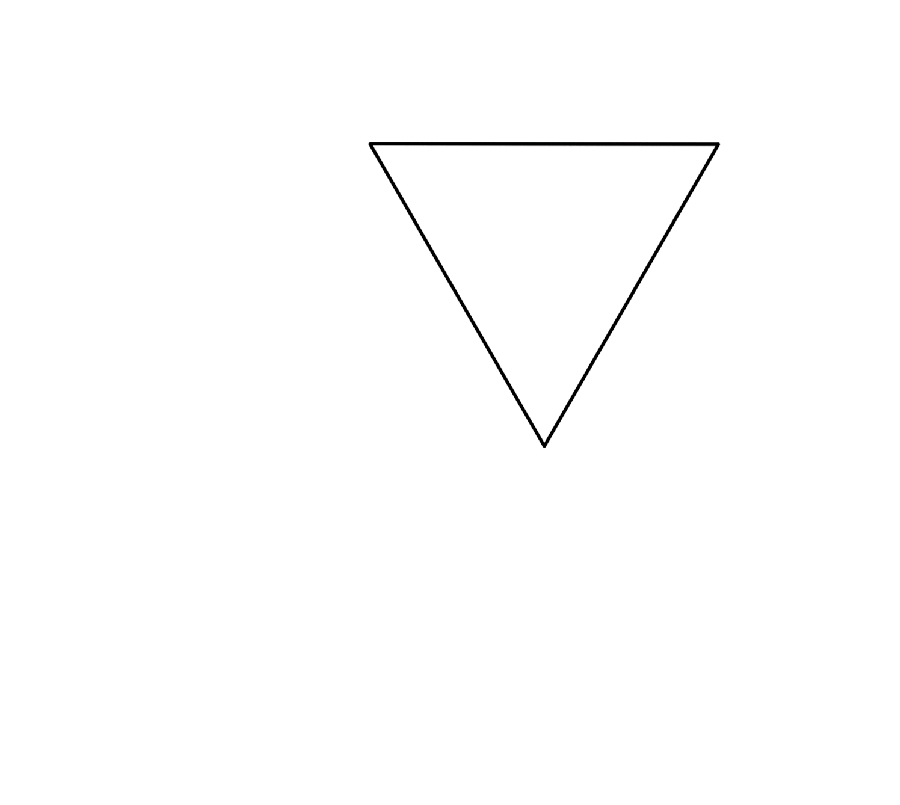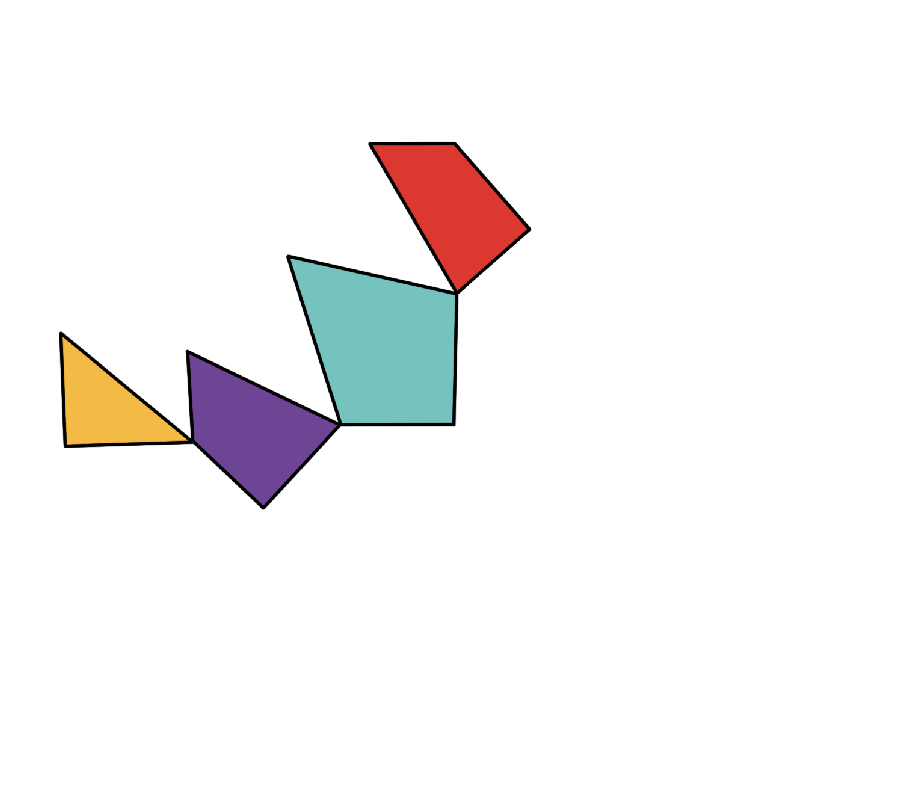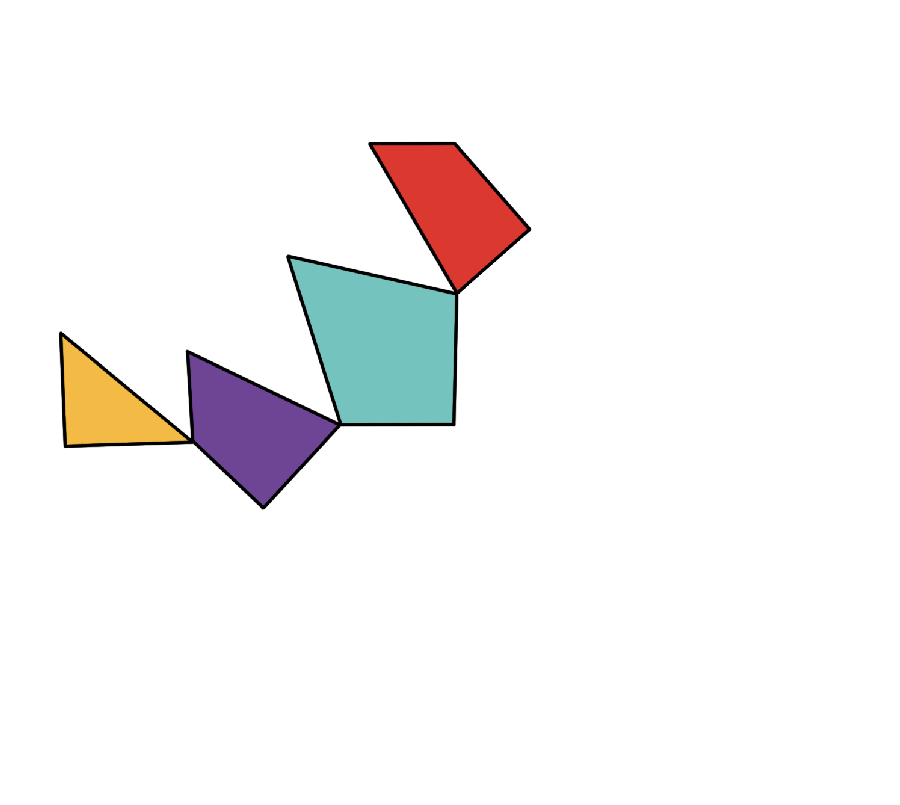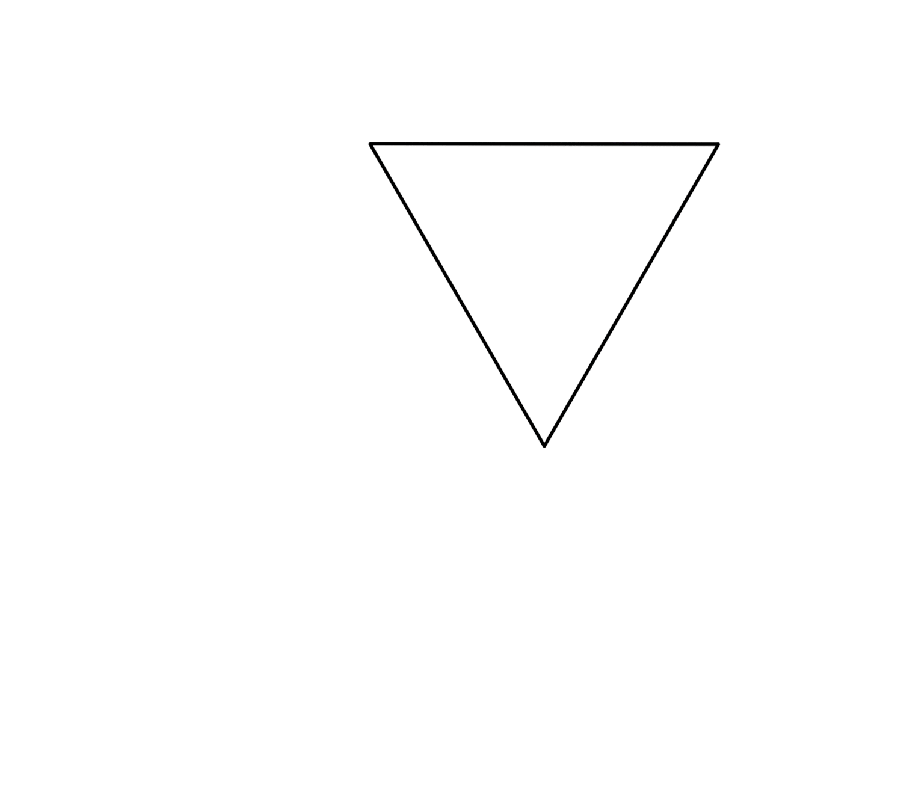
The exhibition explains the origins of a math puzzle published in 1902 newspapers. Henry DudeneySelf-taught English mathematician and puzzle The column, asked readers to discover a equilateral triangle to the smallest piece that could reorganize the square. In his next column, “Mr. Manchester was said. After another two weeks, Dudeney reported that he had not given a solution, and has been recorded, however, whether the solution with fewer pieces existed.
To help Science Journalism
If you enjoy this article, consider entering award-winning journalism Subscribe. By purchasing subscription, you are helping to ensure the future of stories about the discoveries and ideas that are conformed to today.
The puzzle was known as “Dudeney’s dissection” or “Haberdasher’s problem”, and also appeared American scientific‘s June 1958 issue. Martin Gardner, magazine mathematician and a long-standing columnist wrote about Quandari.
(Test American scientificMath puzzlesDiagnies
Now, after proposing more than 122 years, Kamato and the other two mathematicians eventually proved that a solution with fewer pieces is impossible. The result was published on the ARXIVER server in December 2024 “Dudeney’s dissection is perfect. “
“Many appreciate mathematics would agree that it is a simpler unresolved problem, the more fascinating it is for those who love math,” says Kamatak.
Massachusetts Institute of Technology Erik Mathematics Mathematical and Ryuhei Uehara mathematician mathematician, developing a new approach to Kamata to deal with the theory of the graphics using origami-fold problems. In the graphic theory, a graph basically lines or edges and edges, are points that meet the edges. The edges and vertices of a graph can be compared with others to study deeper relationships between two structures, Kamata believed a view that can help repair Dudeney’s dissection.
A part of the problem is quite easy: two-piece solution can be discarded by thinking about the limits of the problem. For beginners, triangles and squares must have the same sites because the pieces are the same. For a plaza, the longest possible cut is through diagonal. A little bit of paper and paper math is unfortunately that the length of the diagonal is too short, from the edge of the same triangle in his area, which regulates two-piece solution.
Prove that three-piece solutions are not quite difficult, and that is the reason for the delay of the century. Although three pieces are a simple puzzle, there are many ways to cut the triangle, according to Demaine. “Each of these pieces can have plenty of edges to many edges and the coordinates of these cuts begin in arbitrary points,” he noted. “You have the following constant parameters when there are plenty of opportunities that are so annoying that are possible. You cannot force it with a computer.”
To deal with the problem, the possible dissection of a technical triangle in the group were classified based on how the cuts cross the edges of the triangle. First, researchers sorted an infinite way to cut the triangle in five single classifications. Then they repeated exercise for a square and found 38 different classifications.
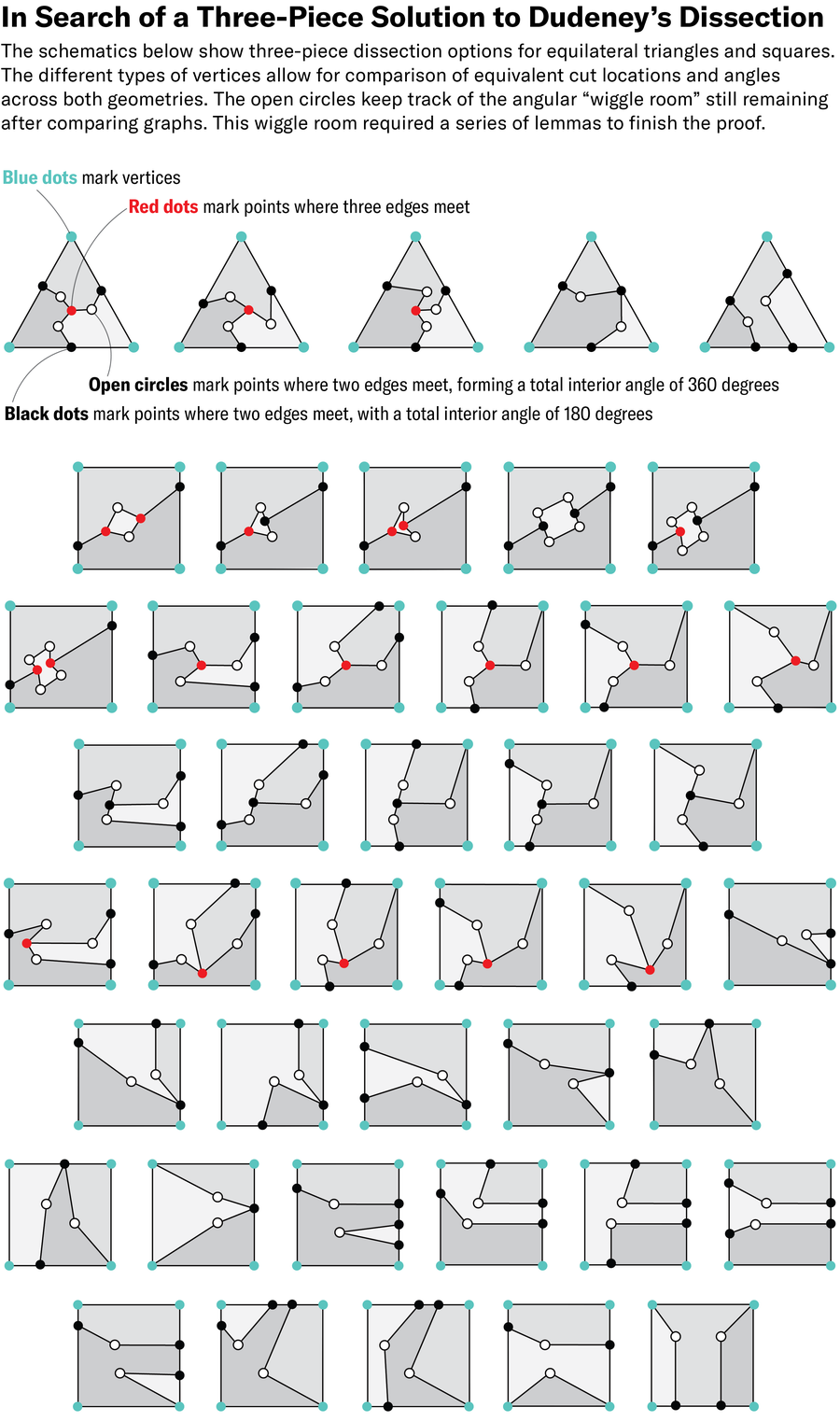
Then the researchers tried to join a triangular square with a square, tracing all possible paths for each form and comparing the collection of edge lengths and angles result. If one of the boxes in the boxes joined a triangle, the researcher meant that they found three-piece solution.
The approach turned the constant problem almost discreet. Within each classification, “there are still many places that can go all these spikes,” Demain says. In the end, the team created the collection of complex lemmas or steps in a theorem, along with categories, finding paths that do not come with contradictions.
Smith College Comport ComportCalist Joseph O’Rourke, who has had Fighting with the puzzle Decades on and off and not involved in current work, he believes that the evidence of the group may probably simplify. He warned that he had taken a confusing collection of very specific Lemma to delete all options, “many other researchers gave up.”
If they lie, the authors have simplified the evidence, the matching diagrams can create open original questions related to the techniques. “These problems remind us that it must be uncovered yet,” Kamatak says. “Anyone can be a pioneer in this limit.”

