The French mathematician Édouard Lucas was born in Amiens in 1842 and died in Paris 49 years later. He wrote a work in four volumes Math gameswhich became a classic of recreational mathematics. In 1883, “N. Claus de Siam” (an anagram of “Lucas d’Amiens”), he marketed a solitaire game called Tower of Hanoi.
He claimed that the game was a simplified version of the so-called Tower of Brahma. In this supposed legend, monks had to move a tower of 64 golden discs in a large temple. Before this task was accomplished, however, the temple would crumble to dust, and the end of the world would come.
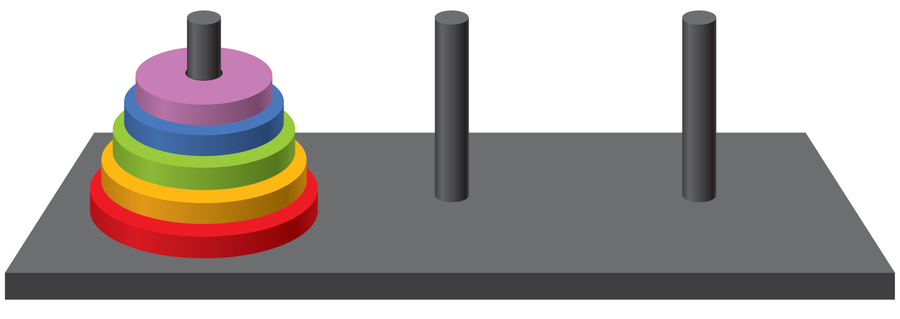
The Tower of Hanoi consists of a small board on which three identical cylindrical rods are mounted. On the left rod are five discs of different sizes with a hole in the middle. They are ordered by size, with the largest disk at the bottom. The object of the game is to move all the discs from the left rod to the right rod in the fewest possible moves. In each move, only one disc can be taken from one rod and placed on another rod, and a larger disc can never be placed on a smaller disc. How many and which movements are needed to transport the discs?
We replace the disks with numbers according to size. We now build the solution systematically, starting with a tower with a single disc. The solution is trivial. With one move you transport a single disk from left to right.

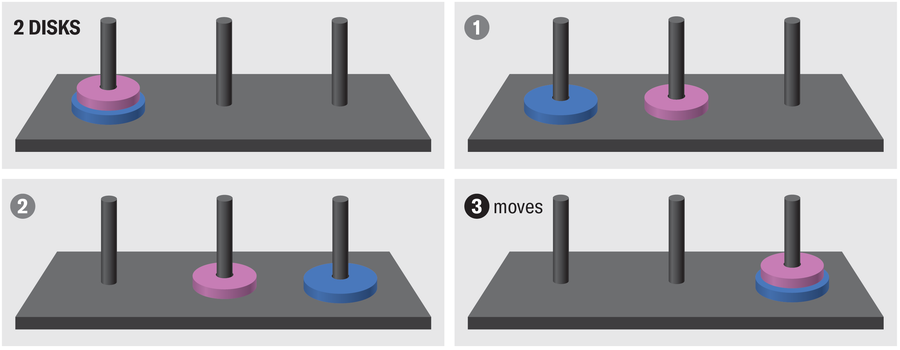
For a tower with two disks you first move disk 1 from left to middle, then disk 2 from left to right and finally disk 1 from middle to right. So you need 3 = 22 – 1 movement.
For a tower with three disks we first mentally exclude the 3rd disk. This reduces the problem to a task involving only two disks, which we now transport from left to center in three moves. With a fourth movement we transport the 3rd disk three times from left to right. Now we mentally leave the 3rd disk out by repeatedly transporting both disks from the middle to the right in three movements. It has a total of 3 + 1 + 3 = 7 = 23 – 1 movement.

The tower problem with four discs can be reduced in a very analogous way to the tower with three discs. So you need 7 + 1 + 7 = 15 = 24 – 1 movement. Finally, for a tower with five disks, you need 15 + 1 + 15 = 31 = 25 – 1 movement. Generally you need 2n – 1 for a moving tower n the discs Édouard Lucas’ original game had eight discs.
We’d love to hear from you! Send to email address games@sciam.com to share your experience.
This puzzle appeared first the spectrum of science and reproduced with permission.

