When I was in high school, I didn’t find math particularly exciting. To be honest, I only learned it when I went to university because it seemed quite easy at first. But in my first math lecture, I realized that everything I knew about math was wrong. Except easy. Mathematics, I soon discovered, can be really exciting, especially if you go beyond the realm of pure arithmetic.
In physics, the really amazing content—concepts that go against your intuition about the universe—emerge around high school, when students can glimpse the strange quantum world and encounter Einstein’s general and special relativity. School mathematics cannot keep up with these miracles. You learn basic arithmetic operations, integration and differentiation, basic handling of probabilities and vectors. If you’re lucky, ambitious teachers will show you a simple proof. And that’s it. So it is not surprising that many students lack a real passion for the subject.
However, mathematics offers all kinds of surprises, for example Banach-Tarsky paradoxit says you can almost magically duplicate a sphere, or that there are infinitely many different ones. What really surprised me was discovering how deeply mathematics is intertwined with the strangest physical phenomena. It is not necessarily quantum physics itself that produces the incredible effects; no, systems always follow the strict rules of mathematics. As chemist Peter Atkins said in his 2003 book Galileo’s finger“Determining where mathematics ends and science begins is as difficult, and as pointless, as mapping the edge of a morning mist.”
About supporting science journalism
If you like this article, please consider supporting our award-winning journalism subscribe. By purchasing a subscription, you’re helping to ensure a future of impactful stories about the discoveries and ideas that shape our world.
Few examples illustrate the intermingling of mathematics and physics better than the discoveries made by physicist Michael Berry. In 1984 Berry revealed a deep and unexpected geometric side of quantum mechanics.. Berry realized that this geometry gives quantum particles a kind of memory.
Nothing really should happen
At the time, Berry was investigating a very simple system: the quantum state of a particle, such as a neutron, in a changing environment. Neutrons have a quantum property called spin, which acts like a tiny magnet that the particles carry with them. That spin can face the north pole up or down; so physicists say that neutrons “spin” or “spin”. The spin of a neutron is affected by external magnetic fields.
Berry used mathematical means to find out what would happen to the neutron if the direction of the magnetic field were slowly changed. According to the so-called adiabatic theorem, which was introduced at the beginning of the 20th century, the quantum properties of the particle should not change as a result: its energy, momentum, mass and spin remain the same.
If you slowly rotate the direction of the magnetic field and then move it back to its original direction, this action should, in principle, not change anything. “That was, at any rate, the prevailing view among physicists for many years,” Berry wrote. in the article American scientific In December 1988. But “the phase shift of a wave function was overlooked.”
One of the strangest phenomena of quantum mechanics is wave-particle duality: quantum objects can be represented as point-like shapes, but they also exhibit wave behavior like water. A phase describes a displacement of the wave at a certain angle; for example, the cosine function is just a phase-shifted sine function.
As Berry recognized in his calculations, a slow change in the magnetic field causes the neutron wave function to rotate in a certain phase. This means that the particle’s wave function shows what happened in the past (in this case, a change in the magnetic field). Furthermore, Berry recognized that this phase does not occur only in the special case of a particle in a magnetic field. Various situations in which a quantum system changes slowly and then returns to its original conditions leave traces in the wave function.
Experiments conducted shortly after the publication of Berry’s pioneering work confirmed these ideas. If you are familiar with quantum mechanics, you probably know that the wave function is not a directly observable quantity. However, there is a way to measure the phase shift using a second particle as a reference. In these experiments, physicists allowed the collision of two particles, such as neutrons, one of which was previously in a changing magnetic field. When the neutrons collided, their wave functions interacted.
These functions act like water waves: if troughs and peaks align, they reinforce each other; on the other hand, if they move against each other, they can be completely weakened or killed. These phenomena are known as constructive or destructive interference, respectively.
Experiments revealed that Berry was correct: the neutrons were out of phase, as destructive interference. That observation indicated that one of the particles was briefly in a changing magnetic field. Although none of its measurable properties changed directly as a result, its wave function did.
The curved universe
But how did Berry know that the particles would undergo a phase change? In fact, such a phase appears where there is curvature. This is why the phase is so important in Einstein’s general theory of relativity—the theory he used to describe gravity.
Some experts argue that general relativity is more geometry than physics. According to this theory, matter bends space-time, and this deformation causes the masses to attract each other—a phenomenon we perceive as gravity. I like to think of it as a sheet of rubber on which heavy objects are placed, deforming the sheet and thus impacting the objects. This visualization has some weaknesses, however: spacetime is two-dimensional in this conception, and I look down from my three-dimensional world. General relativity, on the other hand, describes the curvature of four-dimensional space-time without looking at it from a five-dimensional perspective.
This raises the question of how you can infer the curvature of something if you can’t look at the object from the outside. Berry’s observed phase helps here.
Suppose I wanted to prove in a complicated way that the Earth is a sphere. For this, I can walk north from somewhere in Germany over mountains, valleys, rivers, lakes and oceans. In this thought experiment, nothing can stop me from following a straight path. When I reach the North Pole I move to the right without turning around like a crab. I walk until I finish at the same latitude where I started. Then I continue along the left latitude – again without turning – until I return to the starting point. Even though I landed in the original place, I no longer look north, as at the beginning, but east. So, this commute has not changed me as a person (except for the physical effort, maybe), however, I have made a certain angle.
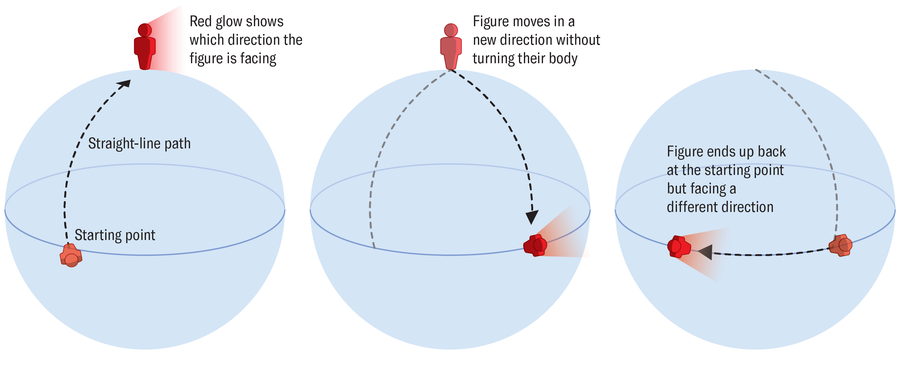
If I had followed the same path on a flat plane, I would have returned to the starting point without any rotation. But in this thought experiment set on our curved planet, the same thing happens to me for the wave function in Berry’s theory: it picks up a phase, an angle that shifts it.
The angle I picked up on my travels depends solely on the Earth’s geometry. Its value is proportional to the area enclosed by my paths. Because nothing else affects the phase—not my speed, not whether I take a break—it’s called “geometric phase.”
For mathematicians, this was not new at the time Berry published his work. They had known about the concept for many decades. But no one applied geometric phases to quantum mechanical processes. The phase of the wave function reveals the geometry of the so-called parameter space. It is an abstract, high-dimensional space that includes all parameters that can affect the wave function (such as magnetic field, energy, location, and velocity). The short-term change in the direction of a magnetic field (or other parameter) describes a closed curve in this space, like my circular path in the world. Since this parameter space is typically curved, this leaves traces in the wave function.
“Geometric phase, then, is the best answer the system can give to ‘what path did the system take in parameter space?'” Berry wrote in 1988. American scientific the article “In this sense it is a kind of quantum ‘memory’.”
Berry revealed a profound connection between quantum systems and geometry, which was very valuable. The eponymous Berry phase can be used to explain phenomena such as the quantum Hall effectwhat happens in certain solids and raised many questions before Berry’s discovery.
This is all very exciting. For me, however, the most impressive thing is that Berry established a new field of research in geometric quantum physics based on existing mathematical concepts. He did not have to add anything new to physics or mathematics; on the contrary, mathematics made it possible to reveal something completely unexpected in physics.
This article originally appeared the spectrum of science and reproduced with permission.

