December 23, 2024
5 read me
A little math can make making holiday cookies a breeze
Making cookies takes time and work. Here’s how to make math a little easier and waste less this holiday season

A cookie cutter that creates a tessellation can save time and use more dough.
When our children were small, we spent a lot of time together in the kitchen together We used the opportunities to teach about hidden science: heat and temperature, fluid flow, density, viscosity, physical changes, chemical reactions, acids and bases. How these properties magically combined to rise cakes with carbon dioxide; we told them about yeast and other interesting microorganisms.
We also talked about math: weights and measures, areas and volumes. It’s a great way to incorporate pizza slices. We enjoyed baking cookies together and used several cookie cutters. Our son loved dinosaurs, so we had dinosaur cookies, but also flowers, hearts, stars and animals. When we used the cookie cutters an interesting invention was created: they left gaps between each shape we cut. To use all the dough, it had to be rolled again. But then it got hot and we had to cool it down before we could cut it again. This took time.
It had to be more efficient way to divide the dough
About supporting science journalism
If you like this article, please consider supporting our award-winning journalism subscribe. By purchasing a subscription, you’re helping to ensure a future of impactful stories about the discoveries and ideas that shape our world.
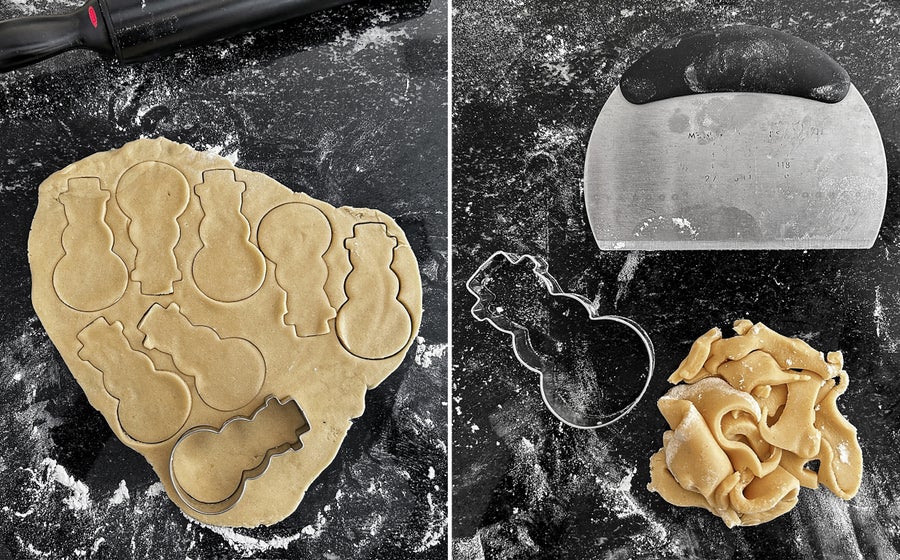
Making cookies using more traditional cookie cutters often leaves a lot of leftover dough.
Being a mathematician, I heard about tile and tessellation, which refer to the covering of a surface using one or more geometric shapes, with no overlaps or gaps. That was the answer to the cookie cutter problem!
So I looked for tessellating cookie cutters, but I could only find squares and hexagons. They work but are not particularly interesting in terms of shapes. And then, about 15 years ago, the first 3D printers arrived. It was possible to make custom cookie cutters, and then it became the choice of shape. Many shapes can be used to tessellate, such as regular or irregular triangles, rectangles, or some irregular pentagons. Some irregular pentagons were discovered by the amateur mathematician Marjorie Rice and can be seen here. Mathematicsan artistic and mathematical exhibition with collaborators including Duke University mathematician Ingrid Daubechies and textile artist Dominique Ehrmann. The exhibit also features a tessellated cookie cutter using the pi symbol, appropriately adapted by Daubechies.
There are other examples; Islamic art includes beautiful and creative designs using pentagonal symmetry.
If we merge two or more images, then there are many more possibilities. For example, octagons and squares, or pentagons and rhombuses, or all the amazing works of MC Escher. But not everyone can make good cookies; We made a cookie cutter in the shape of an Escher lizard but the legs broke when we separated the images.
All these tessellations are periodic, meaning they have a repeating pattern. In the 1970s Roger Penrose discovered two figures called kites and darts that tile a plane only aperiodically (meaning that all possible configurations are non-periodic) if certain local rules are obeyed that determine which sides of the dart they can touch. But if the rules are not followed, they are regularly signed. And that’s perfect for cookie cutters, because the raw dough is regularly tiled, and then the cookies can be placed regularly or not regularly. There is more information about Penrose tiles in the video channel Veritasius and on the web page “A Penrose-type inter-Islamic admixture model“.

A tesselating cookie cutter, such as a kite and dart, creates a nice pattern and uses more dough than other shapes.
A couple of years ago, using a 3D printer, with a lot of help from my friends, I made a kite and dart shaped cookie cutter as I regularly make tiles. After baking, the pieces can be placed regularly or not regularly. This worked beautifully.
And then the Hat arrived.
For some 50 years, mathematicians wondered if there could be a single figure tiling a plane aperiodically. And in 2023 David Smith, Craig Kaplan, Chaim Goodman-Strauss and Samuel Myers managed to find the elusive aperiodic monotile, which they called “The Hat” or “”.einstein“.
My first impulse was to make a hat-shaped cookie cutter. It was very difficult to place the pieces without gaps or overlaps. But those who discovered the Hat also realized that it could be transformed into an infinite number of aperiodic monotiles, as mentioned. Craig Kaplan. All three monotiles can tile regularly and non-regularly, and are perfect in cookie-cutter mode.
Smith and crew called “Tile (0,1)” a chevron that’s easy to make, easy to use in dough, and easy to bake cookies with beautiful patterns, especially if they’re decorated with different colors. Another perfect candidate is what the authors called “Tile (1,1)”. Tiles this image periodically when combined with the mirror image, but only periodically if the mirror image is not supported. Therefore, the perfect cookie cutter has two images, one normal and one mirrored.
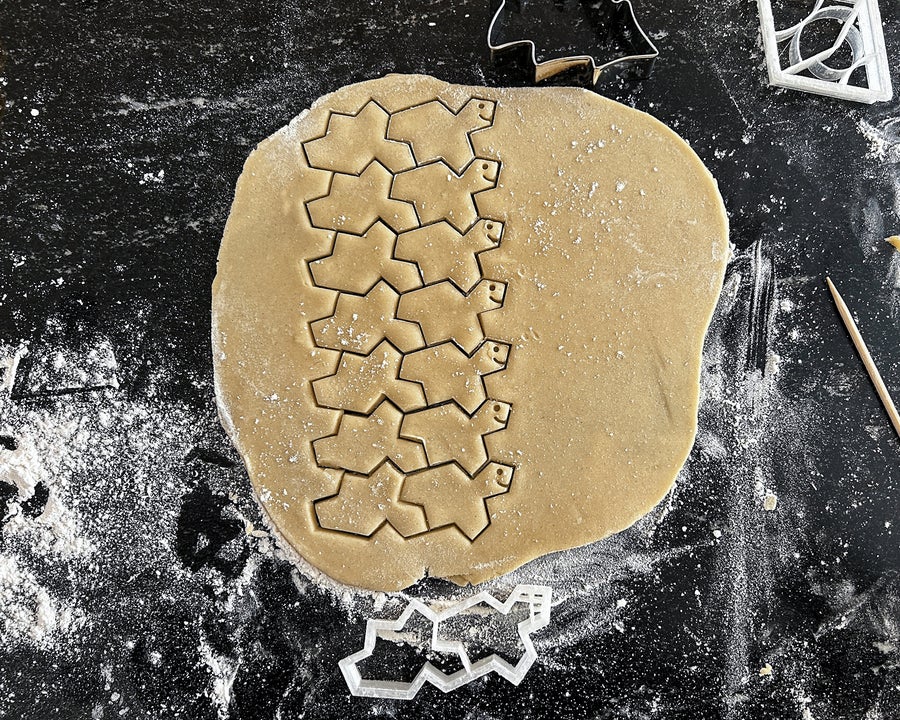
A Hat-based cookie cutter invented by David Smith makes a tessellation pattern that wastes little dough.
Smith and collaborators also invented a category of curved aperiodic monotiles, which they called “Spectres”, which could also be made into cookie cutters, as they recently discovered. soft cells. In each of these cases, if you’re careful, you can cut your cookie dough with minimal rolling and waste.
While you’re cooking and baking for the holidays, if you find a tesselating cookie cutter and get your kids involved, you can take the time you’d spend rolling dough to talk about science and math. In our case, our children are grown, but my tesselated cookie collection and I are excited to share the wonders of math and science when my grandchildren arrive.
This is an opinion and analysis article, and the views expressed by the author(s) are not necessarily their own. American scientific

